四大力学都有其经典与量子相对应。经典力学对应量子力学，经典电动力学对应量子电动力学，经典统计力学对应量子统计力学，经典场论对应量子场论。唯一的例外就是经典热力学，目前通常的物理专业课程中还没有量子热力学。
在国际单位制中有7个基本单位，其中6个已经可以在微观的原子层面定义。唯一的例外是温度，定义它所采用的玻尔兹曼常数，或者水的相变点，是相对宏观的。我们还无法采用一个更加微观的实验手段来定义温度。
按照热力学的语言，温度反映的是分子的平均动能，而那些难以定义动能的系统，比如自旋系统，它的温度依赖性在这个定义下显得非常晦涩。又或者按照能均分定理，每一个自由度贡献，对于较为复杂的大分子，这个定义也是失效的。系综理论将系统的温度归结为由环境来决定，但环境本身是一个相对模糊的概念，环境的温度由谁来提供，没有解释。
归根结底，熵难以被实验测定是根本原因。因为强度量一般难以向微观推广，除了温度，压强、化学势的测定方法也相对宏观唯象。作为与温度相对应的广延量，如若熵能在微观层面被准确测定，我们就可以利用能量对熵求导来获得温度。然而经典统计力学利用状态数来定义熵，令这一想法难以实施。

近年来，伴随着量子信息的迅速发展，测量纠缠熵已经不存在原则性的技术障碍。是否能够利用这一新技术来重新诠释热力学中的温熵关系呢？这就涉及如何在量子力学框架内重新定义热，量子热力学这一古老命题因此重焕生机。

曾经，苏联在热力学的研究中走在世界前列。在朗道的唯象理论中，自由能是热力学的核心物理量，所有系统都要向自由能最小的状态演化，正如力学系统总会选择作用量最小的运动路径一样。而自由能是温度的函数，只要能准确测量自由能，温度的确定就是题中应有之义。自由能是刻画热平衡状态的特性函数，按照导出经典涨落—耗散定理的惯例，我们需要找到一个能将平衡态与非平衡态联系起来的办法。20世纪90年代发展起来的量子涨落理论，就是在平衡态的自由能与非平衡态的不可逆功之间建立联系，从而通过测量功来确定自由能。
对于一个绝热系统，如果其能级从E_n跃迁到E_m，则可以定义外界对其做功为W=E_m-E_n。现若假定跃迁的初态和末态均处于热平衡状态，并且跃迁过程发生的概率分布函数为R(W)，利用细致平衡原理不难推得所谓的Crooks关系^[1]：

其中ΔF是末态与初态的自由能之差，R' 为反向做功概率。这个关系中做功会发生涨落，因为功是与路径有关的过程量，所以如果我们对所有可能的做功路径取平均，就得到著名的Jarzynski等式^[2]：乍一看，Jarzynski等式与经典热力学中自由能与做功最小值的关系有相似之处，然而经典热力学的自由能需要在近平衡状态讨论，以确保整个过程可逆。Jarzynski等式对可逆性不做要求，任意偏离的平衡态原则上都是允许的。当然，e指数必然会放大实验测量时的误差，导致某些反向做功的路径影响更加显著。

在Jarzynski等式被提出来以前，人们更多的是采用路径积分对自由能的处理方式，也就是将温度看作虚时间，并将其作为演化的另一个维度。这跟经典热力学的定义并不自洽，因为等温—绝热过程在卡诺热机中被认为是可逆的，它无法用来定义时间之矢。如今我们在量子涨落理论的框架下，利用不同能级状态之间相干性的变化，可以将温度之矢定义为量子系统的固有演化方向，从而为热的量子化提供新的诠释，这正是下面要谈的量子资源论的主要研究思想。
2002年发表在Science杂志上的一个工作验证了Jarzynski等式^[3]。他们利用纯机械的方法将折叠的核糖核酸强行展开，通过测量施加的力来确定相应的功，并与自由能对比。此后，在蛋白质、聚合物、冷原子、离子阱等诸多实验体系中，均以不同形式验证了这一等式的合理性。笔者认为，Jarzynski等式是量子热力学一个很好的切入点，未来我们不妨用DNA或其他更具标志性的生物大分子作为测量自由能的“标准器”，并据此定义更加微观的温度，作为基本物理量使用。

自伽利略发明温度计至今，人类对于温度的研究已有四百多年，早于电、磁、光等其他学科。从热电偶到红外线，人类的测温手段日益丰富，然而横向对比其他几门学科，电已能够小到皮安，磁已能够弱到高斯，光已能够短到阿秒，而即使目前最先进的测温控温设备，其温度仍在小数点后第一位来回跳动，和四百年前几无进步。发展新的微观测温方案，我们需要全新的理论框架。

量子热力学最核心的理论体系是在量子混沌理论的基础上建立起来的，目前常见的文献中，关于量子混沌的名称通常表述为quantum chaos^[4]。Berry当年曾使用quantum chaology，用以区分全量子系统的混沌效应，这个词偶尔会出现在文献中，但未广为接受。我们现在通常研究的量子混沌，是指将量子系统经典化或半经典化后的混沌，后者是指将原子核部分经典化，再与经典混沌相比较。全量子系统的混沌研究目前未有重大进展。

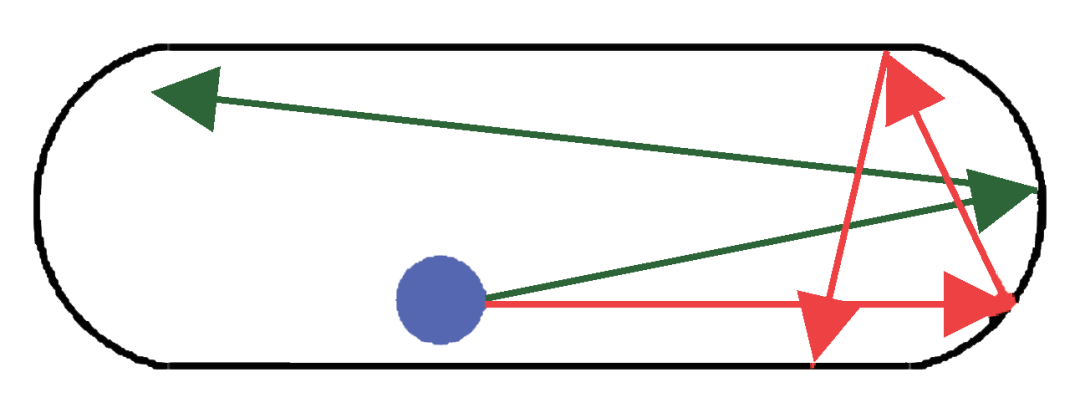
在经典力学中，与混沌相对应的概念是可积。当一个运动系统的自由度与守恒量(运动积分)的数量一致时，其运动方程是可积的(可解的)。相反，若找不出足够数量的守恒量，则该系统是混沌的。一般地讲，由于能量守恒总是先验成立，故而一维经典体系总是可积的。若再加上角动量守恒，则二维体系也可积，比如开普勒行星模型。但若二维体系有特殊的边界，比如图1所示的是混沌理论中经常作为出发点的L. A. Bunimovich体育场(stadium)模型^[5]，其形状如一个田径运动场，这种情况下无法找到第二个守恒量，则会出现混沌。除此以外，非微扰三体系统也因找不到足够的守恒量而成为混沌，比如水分子的三个原子、质子的三个夸克等，这是流体力学、核物理中时常发生混沌现象的原因。至于三维，不可积的情况更为常见，所以绝大多数自然系统都是混沌的，可积系统只是少数。

ETH和经典统计中的各态历经假说究竟有什么不同？笔者认为，ETH最大的优点并不在于它描述了“绝大多数”系统的行为，而是它给出了不满足各态历经的明确条件。各态历经虽然是经典统计的基本假定，但它不同于其他物理理论，其预测性差，又难以证伪，总是会产生各种似是而非的结果。而在ETH的定义中，对于先验成立的各态历经假说，我们有了可以定量证伪它的方案，这是了不起的进步。

作者：姚尧

(华南理工大学物理与光电学院)

本文选自《物理》2024年第2期